Diseño de cascadas sin espesor
Autor/a, Autores/as: Galindo Lucas, José
Introducción
El funcionamiento de las turbomáquinas viene determinado por la geometría del espacio anular (diseño meridional) y de los perfiles y disposición de los álabes. Esta aplicación permite visualizar la geometría de las cascadas en función de:
- Los ángulos del perfil en el borde de ataque \(\displaystyle {\varphi _1} \) y el borde de fuga \(\displaystyle {\varphi _2} \) del perfil. La suma de los valores absolutos de ambos ángulos definen el llamado ángulo de curvatura \(\displaystyle {\varphi}{=}{\left|\varphi _1\right|+\left|\varphi _2\right|} \) que es el parámetro más importante en la definición del perfil.
- La solidez \(\displaystyle {\sigma} \): se trata de la relación entre la cuerda (distancia entre borde de ataque y borde de fuga del álabe) y el paso (distancia entre los bordes de ataque de los álabes una vez montados en la cascada.
- El ángulo de calado \(\displaystyle {\gamma} \): se trata del ángulo formado entre la cuerda del perfil y la dirección axial (paralela al eje de la turbomáquina).
Si consideramos la hipótesis de que la incidencia y la desviación son nulas, entonces los ángulos de las velocidades del flujo de entrada y salida de la cascada coinciden con los ángulos de los álabes \(\displaystyle {\beta _1} \) y \(\displaystyle {\beta _2} \).
Si consideramos además que la velocidad meridional \(\displaystyle w_m \) se mantiene uniforme a lo largo de la cascada podemos estimar las velocidades del flujo a la entrada \(\displaystyle {w_1}{=}{w_m}{/}\cos \beta _1 \) y a la salida \(\displaystyle {w_2}{=}{w_m}{/}\cos \beta _2 \). La evolución de la velocidad meridional desde la entrada hasta la salida de la cascada es independiente del diseño y montaje de los perfiles. Solamente depende de la evolución del área del espacio anular.
Con las hipótesis anteriores podemos determinar el carácter de la cascada diseñada solamente a partir de los ángulos de entrada y salida de la cascada. La cascada se llama aceleradora cuando aumenta la velocidad del flujo (\(\displaystyle {w_2 > w_1} \)), o sea, cuando \(\displaystyle {\left|\beta _2| > \right|\beta _1|} \). La cascada se llama difusora cuando reduce la velocidad del flujo (\(\displaystyle {w_2 < w_1} \)), o sea, cuando \(\displaystyle {\left|\beta _2\right| < \left|\beta _1\right|} \). Cuando \(\displaystyle {\left|\beta _2\right|=\left|\beta _1\right|} \) la cascada no acelera ni decelera el flujo, sería el equivalente a un conducto de sección constante. \(\displaystyle \)
Objetivos
El objetivo de este objeto de aprendizaje es que los alumnos de turbomáquinas sepan relacionar las características geométricas básicas que definen una cascada de álabes de una turbomáquina con el efecto que va a producir en términos de aceleración o deceleración del flujo que la atraviesa. Se contempla en este objeto de aprendizaje el caso de álabe sin espesor para destacar la importancia de los ángulos de curvatura del álabe y de calado con el que el álabe se monta en la cascada, por encima de la definición del tipo de perfil de álabe utilizado.
Instrucciones
Se propone seguir la siguiente secuencia para identificar cómo afecta cada uno de los parámetros de diseño en el resultado final de la cascada generada:
- La simulación se inicia con un perfil sin curvatura, como una placa plana, con un ángulo de calado nulo, una solidez unitaria y un perfil simétrico. Se propone modificar calado y solidez y observar las cascadas generadas. En todos los casos se obtienen cascadas de sección constante.
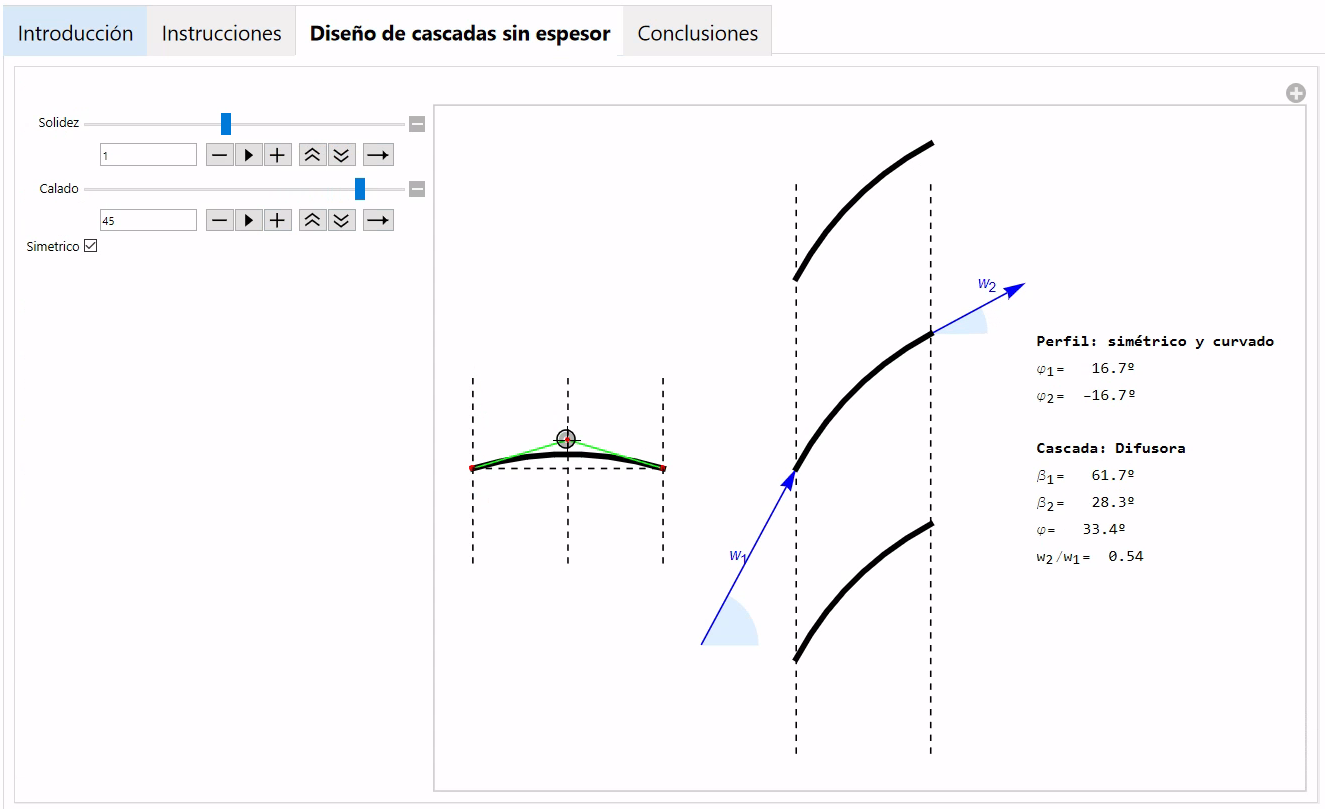
- A continuación se propone modificar la geometría del perfil para obtener un álabe curvado. Para ellos hay que actuar sobre el punto de control en la imagen del perfil aislado. Una vez definido el nuevo perfil, se propone modificar calado y solidez para observar las cascadas generadas. En álabes con curvatura ya aparecen cascadas aceleradoras y difusoras. La magnitud de la aceleración-deceleración se cuantifica con el parámetro factor de difusión \(\displaystyle {w_2/w_1} \) que es mayor que 1 para una cascada aceleradora y menor que 1 para una difusora.
- Es importante destacar que la curvatura del perfil aislado puede hacerse por encima o por debajo de la cuerda. Al cambiar esta característica, cambia el carácter de la cascada generada. Una cascada aceleradora se convierte en difusora y viceversa. Sin embargo, dos perfiles con las curvaturas en sentido opuesto, pueden producir el mismo diseño si se cambia también el signo del ángulo de calado. Se propone encontrar cascadas idénticas a partir de un perfil aislado con la misma curvatura pero orientada en sentidos opuestos.
- Se propone por último desactivar la casilla Simétrico que permite obtener diseños de perfil en los que la flecha máxima no está en mitad de la cuerda. Esto produce álabes en los que \(\displaystyle \left|\alpha _1\right|\neq \left|\alpha _2\right| \), por lo tanto álabes que no son simétricos con respecto al eje vertical en mitad de la cuerda. Se propone por un lado, partiendo de una cascada definida con perfil simétrico modificarla y ver cómo se modifica el factor de difusión. Por otro lado se propone comparar diseños de perfil cambiando la posición de la flecha máxima, pero manteniendo constante el ángulo de curvatura.
Laboratorio virtual
[Pulse sobre la imagen del laboratorio para descargarlo y ejecútelo posteriormente en el “Wolfram CDF Player”]
NOTA: Si no tiene instalado todavía el “Wolfram CDF Player” debe descargarlo e instalarlo previamente en su ordenador para poder ejecutar el laboratorio. Pulse aquí para acceder a la “Wolfram CDF Player”.
Conclusiones
En esta aplicación se ha mostrado la influencia de la geometría del perfil, el ángulo de calado y la solidez, en las características de la cascada resultante.
De estos 3 parámetros, el más decisivo es el ángulo de calado \(\displaystyle {\gamma } \), ya que en función de su signo la cascada resultante va a ser aceleradora o difusora.
El siguiente parámetro por orden de importancia es el ángulo de curvatura del perfil \(\displaystyle {\varphi } \). Al aumentar la curvatura del álabe se aumenta el efecto de aceleración o deceleración que produce la cascada, salvo que el ángulo de calado sea nulo.
A continuación, se destaca la forma del perfil. Se pueden distiguir perfiles simétricos en los que la flecha máxima del perfil está en la mitad de la cuerda (\(\displaystyle \varphi _1=-\varphi _2 \)), o perfiles asimétricos en los que la flecha máxima se acerca al borde de ataque. Este parámetro puede tener relevancia en cómo se realiza el proceso de aceleración-deceleración dentro de la cascada. Pero en primera aproximación, el comportamiento de la cascada viene determinado por los valores de los ángulos \(\displaystyle {\beta _1} \) y \(\displaystyle {\beta _2} \), y no por la evolución entre uno y otro dentro de la cascada.
Por último, la solidez no tiene efecto ninguno sobre los ángulos de la cascada ni sobre el factor de difusión resultante.
- El diseño típico en cascadas de compresores axiales es: álabe simétrico; curvatura entre 20 y 40º; ángulo de calado alrededor de 45º y solidez entre 0.5 y 1.5.
-
Los diseños típicos en cascadas de turbinas axiales son dos:
- Estator de turbina de acción o estator/rotor de reacción: álabe asimétrico con flecha máxima entre del 20 y el 30% de la cuerda; curvatura entre 60 y 90º; ángulo de calado alrededor de 35º y solidez entre 1 y 2.
- Rotor de turbina de acción: álabe simétrico; curvatura entre 90 y 140º; ángulo de calado 0º y solidez entre 1.5 y 2.5.